1970 : un mathématicien crée un "jeu" avec des points sur une grille. Cette récréation va révolutionner l'informatique, la biologie et notre compréhension de l'univers. Son nom ? Le "Jeu de la Vie". Liverpool, 1937. John Horton Conway naît dans une famille modeste. Il étudie au Gonville and Caius College de Cambridge, où il obtient son doctorat en 1964. À Cambridge, il devient un membre éminent du groupe de théorie des nombres. Ses premières recherches portent sur la théorie des groupes finis, où il fait des découvertes majeures sur les groupes sporadiques (des structures mathématiques si complexes qu'on les surnomme "monstres"). 1970 : sur les ordinateurs de Cambridge, il développe le "Jeu de la Vie", un automate cellulaire dont les règles simples produisent une complexité extraordinaire. La publication de ses règles dans Scientific American le rend célèbre bien au-delà du monde mathématique. Sur une grille infinie, chaque cellule peut être dans deux états : vivante ou morte. Les règles exactes sont : 1. Survie : une cellule vivante avec 2 ou 3 voisines vivantes survit à la génération suivante 2. Naissance : une cellule morte ayant exactement 3 voisines vivantes devient vivante 3. Mort : dans tous les autres cas, la cellule meurt ou reste morte (solitude ou surpopulation) Ces règles simples créent des comportements complexes et documentés : MOTIFS STABLES : - le "bloc" (carré de 4 cellules) - la "ruche" (hexagone de 6 cellules) - le "bateau" (forme de bateau de 5 cellules) OSCILLATEURS : - le "clignotant" (3 cellules qui alternent entre vertical et horizontal) - le "planeur" (5 cellules qui se déplacent en diagonale) - le "canon à planeurs" (configuration qui émet régulièrement des planeurs) De 1964 à 1986, il est chercheur puis professeur à Cambridge. Il y développe plusieurs théories fondamentales : - les nombres surréels, une extension révolutionnaire des nombres réels - la théorie des jeux combinatoires - une nouvelle notation pour les grands nombres 1986 : il devient professeur à Princeton, où il occupera la chaire John von Neumann. Son style d'enseignement est réputé pour rendre accessibles les concepts les plus complexes. Ses contributions majeures incluent : - l'algèbre des quaternions - la théorie des nœuds - l'étude des pavages du plan - la classification des groupes finis simples 2017 : publication de son autobiographie "Genius At Play", qui documente sa vision unique des mathématiques. 11 avril 2020 : Il décède à Princeton des suites du COVID-19. PS: le "Jeu de la Vie" est aujourd'hui considéré comme l'un des premiers exemples d'émergence de complexité à partir de règles simples, un concept fondamental en sciences.

Il est temps de remplacer π ! Tout le monde connaît π, cette fameuse constante d’environ 3,14. On l’a apprise à l’école, elle est omniprésente en maths et en sciences. Mais on utilise depuis des siècles la mauvaise constante ! Oui, tau (τ) est bien plus naturel que π, et voici pourquoi. Rappelons nous d'où provient π. Le cercle est au cœur de la définition de π : on le définit comme le rapport entre la circonférence et le diamètre, soit π = C/D. Pour rappel, le diamètre est 2r et la circonférence (périmètre) du cercle est 2πr donc C/D =2πr/2r=π. Autrement dit, π correspond à un demi cercle. Mais en réalité, le diamètre n’est pas la mesure la plus naturelle du cercle, c’est le rayon qui l’est. On a vu que la circonférence du cercle est : C=2πr Pourquoi garder ce facteur 2 ? En définissant τ = 2π ≈ 6,28, on obtient tout simplement : Ce qui est bien plus élégant et naturel. Et c'est plus logique pour les angles ! En maths, on utilise beaucoup plus souvent les radians pour mesurer les angles. Avec π, un tour complet est 2π radians, un demi-tour est π radians, un quart de tour est π/2 radians, etc. Rien de très intuitif. Avec τ, un tour complet est τ radians, un demi-tour est τ/2, un quart de tour est τ/4, ce qui correspond directement aux fractions de tour. Facile à retenir, facile à comprendre. En en plus, la plus belle équation au monde devient encore plus belle ! La formule d’Euler : actuellement écrite e^(iπ) + 1 = 0 devient e^(iτ) = 1, ce qui exprime directement la rotation complète dans le plan complexe. Mais bon, l'adoption de τ n'est pas pour tout de suite... Pourquoi ? L'histoire et l’habitude. π est enseigné depuis des siècles, inscrit dans tous les manuels et logiciels. Mais comme pour toutes les révolutions, il faut briser les conventions ! Je propose qu'on commence tous par ne plus aller faire ππ mais plutôt (τ/2)*(τ/2) ! ------

https://www.garnier-malet.com/....dedoublement-espace-

"La vie est omnipériodique" Une recherche mathématique a duré presque un demi-siècle a pris fin. Dans Game of Life de Conway, une grille infinie de cellules carrées évolue à partir de leur état initial en suivant une règle simple, chaque cellule est dans l'un des deux états distincts : vivante ou morte. Si une cellule morte a exactement trois voisins vivants elle devient vivante, sinon elle devient morte. Le jeu se déroule dans un univers informatique appelé automate cellulaire et passe par un comportement qui montre un motif qui se répète après un nombre fixe de générations ; cela signifie que pour une période donnée (ou un nombre de générations) un oscillateur émerge. Comme les moyens de calcul sont devenus plus puissants, tous les générateurs ont été trouvés. Cette découverte prouve que la Vie en tant qu'automate cellulaire est omnipériodique ce qui signifie qu'elle a un motif qui se répète après un nombre fini de générations. https://arxiv.org/pdf/2312.02799

Pourquoi les mathématiques sont-elles importantes dans les technologies d’aujourd’hui ? Crédit d’image : Propriétaires respectés Plongez dans le monde des chiffres et découvrez pourquoi les mathématiques sont le cœur des technologies d’aujourd’hui ! Qu’il s’agisse d’alimenter des algorithmes ou de façonner l’analyse des données, son importance est inégalée. Voici pourquoi vous ne devez pas négliger son importance : 1️⃣ Résolution de problèmes : Les mathématiques vous apprennent à penser de manière critique et à résoudre des problèmes complexes, une compétence vitale dans tout domaine technologique. 2️⃣ Algorithmes et codage : Derrière chaque application, site Web ou logiciel se cache des algorithmes complexes, tous construits sur des principes mathématiques. 3️⃣ Analyse des données : À l’ère du Big Data, la compréhension des mathématiques est cruciale pour interpréter, analyser et tirer des informations de vastes ensembles de données. 4️⃣ Apprentissage automatique et IA : L’épine dorsale de l’apprentissage automatique et de l’intelligence artificielle est constituée de modèles mathématiques et d’algorithmes, qui façonnent l’avenir de la technologie. 5️⃣ Innovation et optimisation : Les mathématiques alimentent l’innovation en permettant des techniques d’optimisation, rendant les processus plus efficaces et efficients. Prêt à vous lancer dans l’aventure mathématique ? Jetez un coup d’œil à ces meilleurs cours gratuits offerts par les meilleurs instituts et instructeurs : 🎓Maths Essentials par l’Imperial College Business School London 🔗https://edx.sjv.io/OrYZEW 🎓Introduction au calcul par l’Université de Sydney 🔗https://lnkd.in/dgGDV9SV 🎓Introduction à la géométrie par SchoolYourself 🔗https://edx.sjv.io/4PaAMn 🎓Introduction à l’algèbre par SchoolYourself 🔗https://edx.sjv.io/dayvrj 🎓Introduction à la pensée mathématique par l’Université de Stanford 🔗https://lnkd.in/dEvse6Qx 🎓Mathématiques pour l’informatique par l’Université de Londres 🔗https://lnkd.in/dN99Mt7A 🎓Compétences en mathématiques en science des données par l’Université Duke 🔗https://lnkd.in/d8wuTfUn 🎓Mathématiques pour l’apprentissage automatique : algèbre linéaire par l’Imperial College de Londres 🔗https://lnkd.in/dVmCN5cn 🎓Algèbre matricielle pour les ingénieurs par l’Université des sciences et technologies de Hong Kong 🔗https://lnkd.in/dBP2VBbN 🎓Les mathématiques derrière Moneyball par l’Université de Houston 🔗https://lnkd.in/dgVeAMe5 Enrichissez votre compréhension et maîtrisez le langage des chiffres ! Cliquez sur les liens ci-dessus pour démarrer votre parcours d’apprentissage dès aujourd’hui. hashtag#mathematics hashtag#technology hashtag#learning hashtag#freecourses

Algorithmique quantique : de l’exponentiel au polynômial. L’informatique quantique, même si elle n’en est encore qu’à ses premiers pas, porte en elle des promesses qui lui ont valu un engouement spontané de la part de la communauté scientifique. Même si la réalisation d’ordinateurs quantiques reste hypothétique à l’heure actuelle (sauf pour des minia- tures), c’est un domaine de recherche qui a été très actif ces quinze dernières années, et pour cause : ces nouveaux concepts permettraient d’accélérer drastiquement des opérations qui coûtent beaucoup trop cher sur nos ordinateurs actuels (on passe d’une complexité exponentielle à une polynômiale, à une très faible probabilité d’erreur près). Après avoir expliqué brièvement en quoi consiste le modèle de l’ordinateur quantique, nous es- saierons de comprendre et d’apprivoiser la nouvelle puissance de calcul qui s’offre à nous par l’inter- médiaire de deux des plus célèbres algorithmes quantiques : l’algorithme de factorisation de Shor et l’algorithme de recherche de Grover. Nous ne présenterons que brièvement le second, le cœur de ce travail étant l’algorithme de Shor.

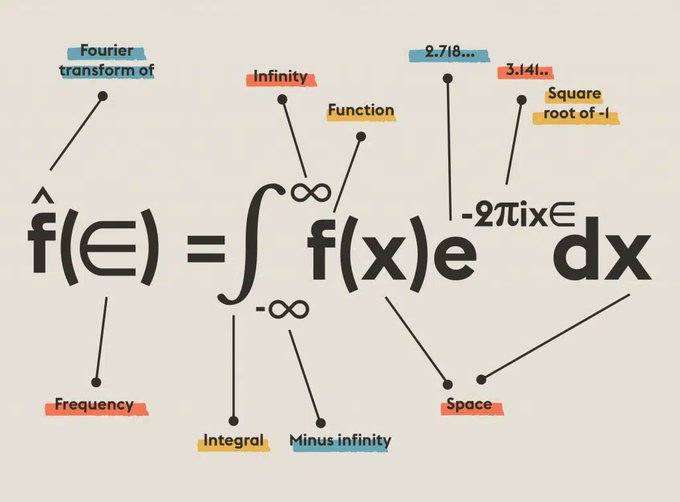
Aujourd'hui, c'est le 256e anniversaire de Joseph Fourier, dont la transformée communément connue sous le nom de transformée de Fourier est utilisée dans : la mécanique quantique, le traitement du signal, la spectroscopie, la compression numérique d'images et de données, la résolution d'équations différentielles, la conception de circuits électriques...

https://www.wolfram.com/broadc....ast/video.php?c=464&

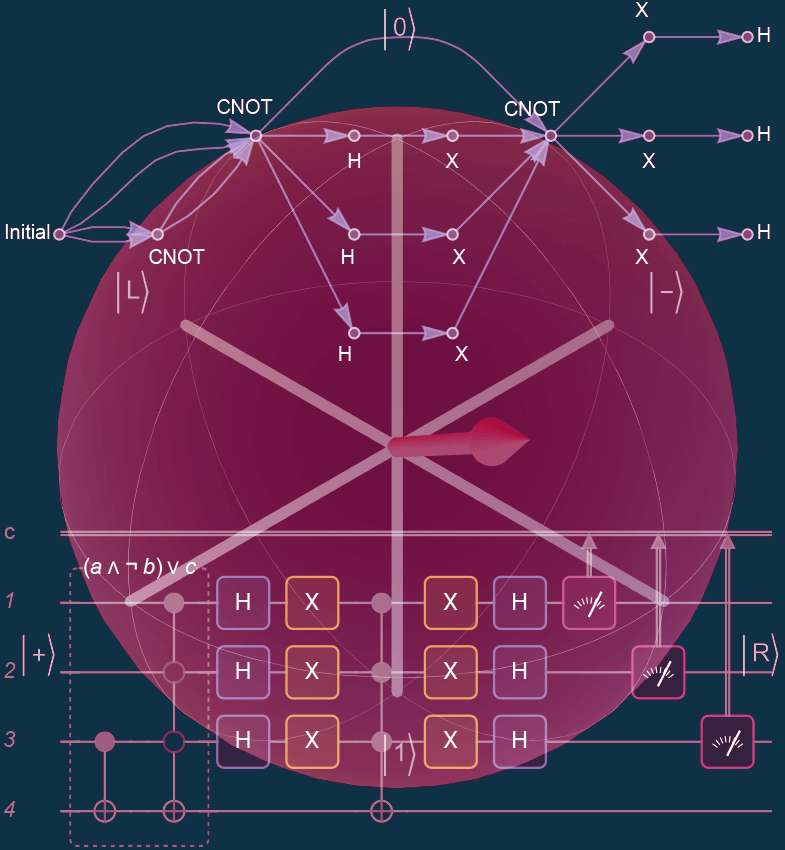
Portes quantiques - Memo. https://www.utc.fr/~wschon/sr0....6/demonstrateur-algo

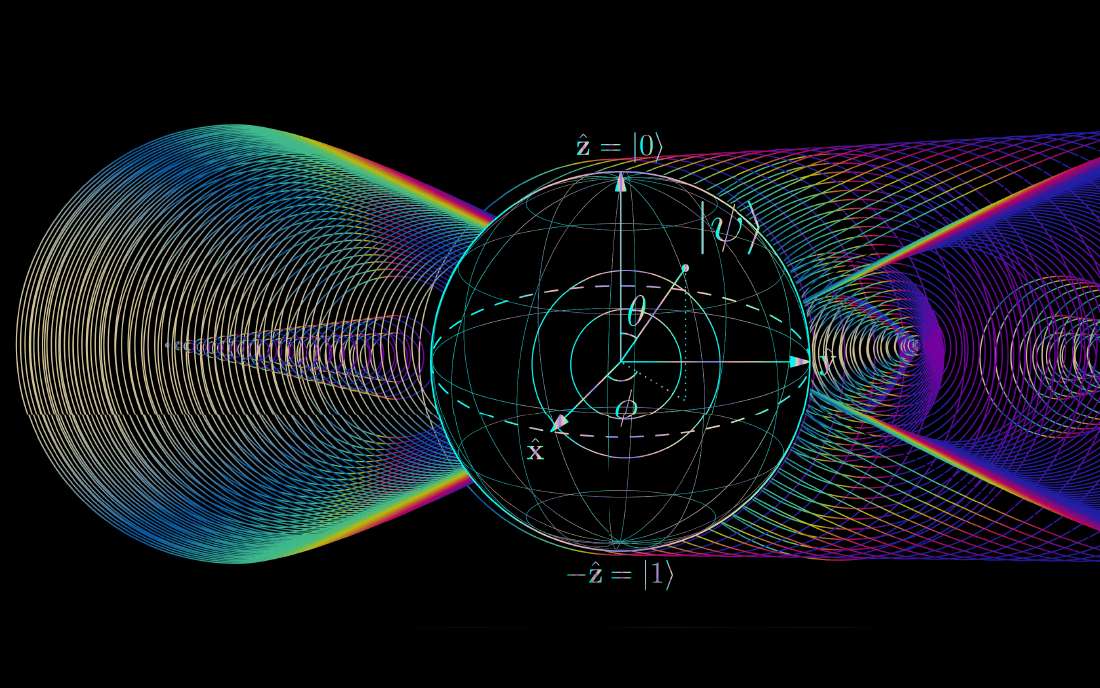
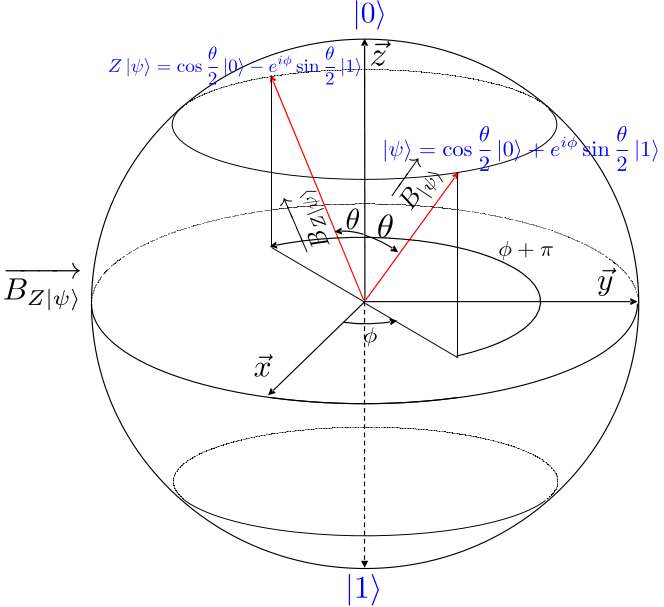
Les portes quantiques à 1 qubit. https://www.utc.fr/~wschon/sr0....6/demonstrateur-algo

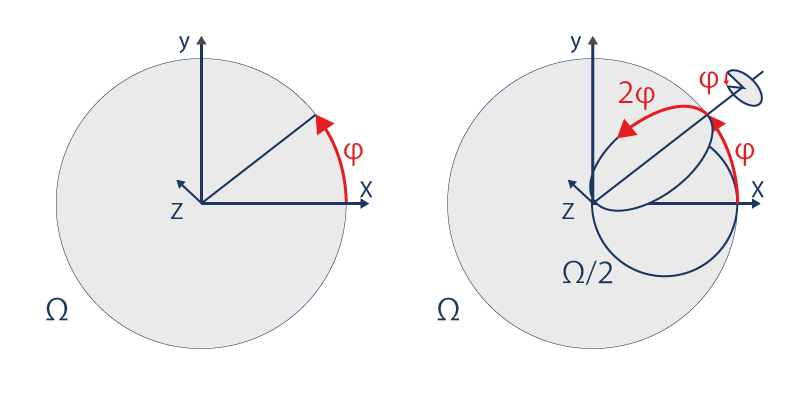
Le polytope 3{3}3{3}3{3}3 C’est un polytope autodual (égal à son réciproque à une isométrie près). Son groupe de symétrie est le 3[3]3[3]3[3]3 d’ordre 155520. Il possède 240 sommets, 2160 arêtes de 3 sommets et 2160 faces de 8 sommets (formant un polygone 3{3}3 et 240 cellules de 27 sommets (formant un polygone Hessien) . La projection utilisée est >Trans:=proc(U) o:=Pi/12; a:=Pi; V:=expand(U[1]*exp(I*a)+(exp(I*(o+a)))*U[2]+exp(I*(Pi/2+a))*U[3]+(exp(I*(-o+a)))*U[4]); [Re(V),Im(V)]; end; http://igm.univ-mlv.fr/~luque/apropos/apropos.html

Detail Description: The specific basis vectors are: x = {1, φ, 0, -1, φ, 0,0,0} y = {φ, 0, 1, φ, 0, -1,0,0} z = {0, 1, φ, 0, -1, φ,0,0} These are 3 of the 4 basis vectors which fold E8 to H4 and H4 Phi. This is constructed from VisibLie_E8 found on TheoryOfEverything.org with the following settings: (* This is an auto generated list from e8Flyer.nb *) new := { artPrint=True; p3D=" 3D"; sliderVal=1.; cylR=0.005; scale=0.042; range=1.7; shwAxes=False; limitToRange=False; showEdges=True; viewAngle=0.4; selPrj="E8->H4"; vp=Join[xyVwPnt={1.11, 2.59},{zVwPnt=-1.86}]; };new; https://en.m.wikipedia.org/wiki/File:E8_3D.png

https://fr.wikipedia.org/wiki/....Construction_des_oct

https://www.techno-science.net..../definition/5052.htm

⁣https://fr.wikipedia.org/wiki/Mathematica

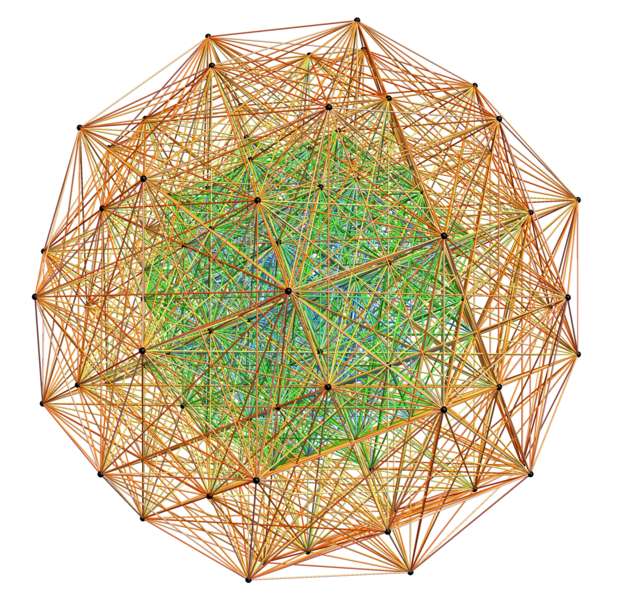
⁣⁣L’empilement des sphères en grande dimension résolu. ⁣Une mathématicienne ukrainienne a résolu un problème vieux de plusieurs siècles, mais en dimensions 8 et 24. https://www.larecherche.fr/mat....h%C3%A9matiques/l%E2

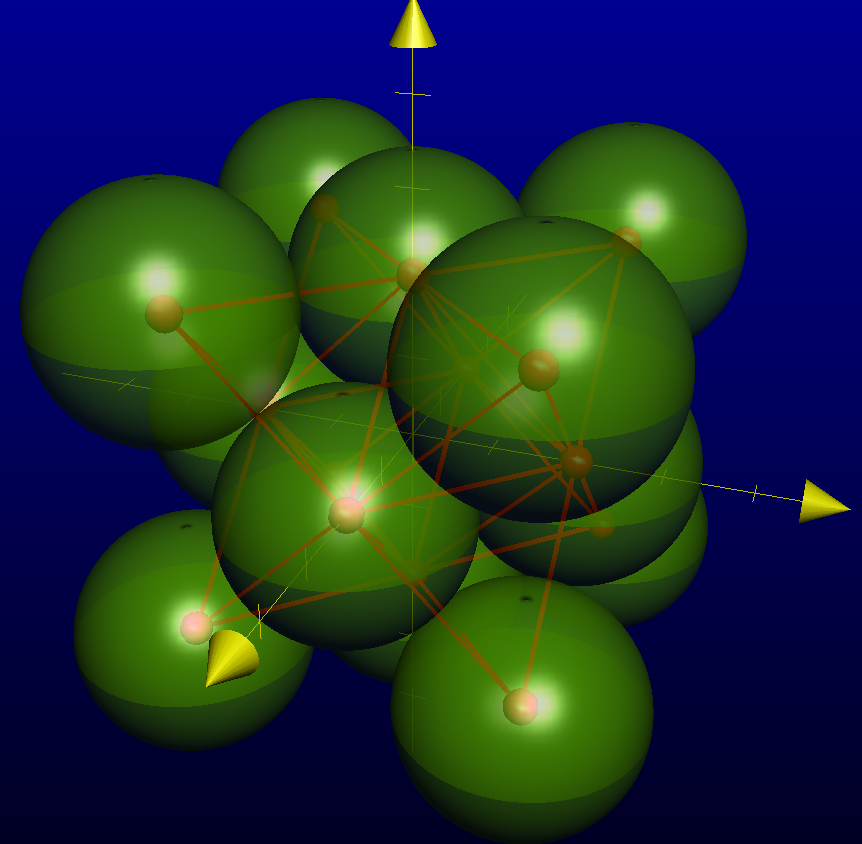
⁣Pe⁣Deepmind, le laboratoire IA de Google, vient de dévoiler AlphaGeometry, un modèle d'intelligence artificielle capable de raisonnement mathématique complexe. Le résultat est réellement stupéfiant.ndant que la bêtise humaine contamine le monde l'intelligence artificielle progresse et repousse les limites. ⁣https://www.clubic.com/actuali....te-515953-google-deg

⁣ https://claude-gimenes.fr/phys....ique/mecanique-quant

⁣ Les chercheurs de l'Université de Californie de San Diego ont trouvé la réponse à r(4,t), un problème de Ramsey de longue date qui perplexe le monde des mathématiques depuis des décennies. Quel était le problème de Ramsey, de toute façon ? En langage mathématique, un graphique est une série de points et de lignes entre ces points. La théorie de Ramsey suggère que si le graphique est assez grand, vous êtes garanti de trouver un ordre à l'intérieur - soit un ensemble de points sans ligne entre eux, soit un ensemble de point avec toutes les lignes possibles entre eux (ces ensembles sont appelés « cliques »). Ceci est écrit en r(s,t) où s sont les points avec des lignes et t sont les points sans lignes. Pour ceux d'entre nous qui ne traitent pas de la théorie des graphes, le problème Ramsey le plus connu, r(3,3), est parfois appelé "le théorème sur les amis et les étrangers" et s'explique par une fête : dans un groupe de six personnes, vous trouverez au moins trois personnes qui connaissent toutes chacun autres ou trois personnes qui ne se connaissent pas tous. La réponse à r(3,3) est six. Que s'est-il passé après que les mathématiciens aient trouvé que r(3,3) = 6 ? Naturellement, ils voulaient savoir r(4,4), r(5,5) et r(4,t) où le nombre de points qui ne sont pas connectés est variable. La solution à r(4,4) est 18 et est prouvée en utilisant un théorème créé par Paul Erdös et George Szekeres dans les années 1930. Actuellement, r(5,5) est toujours inconnu. Un bon problème riposte Pourquoi quelque chose de si simple à affirmer est-il si difficile à résoudre ? Il s'avère être plus compliqué qu'il n'y paraît. Disons que vous saviez que la solution à r(5,5) se situait entre 40 et 50. Si vous commenciez avec 45 points, il y aurait plus de 10234 graphiques à prendre en compte. En 1937, Erdös découvrit que l'utilisation de graphiques aléatoires pouvait donner de bonnes limites inférieures aux problèmes de Ramsey. Ce que Verstraete et Mubayi ont découvert, c'est que l'échantillonnage à partir de graphiques pseudorandoms donne fréquemment de meilleures limites sur les nombres de Ramsey que les graphiques Ces limites - limites supérieures et inférieures de la réponse possible - ont resserré la gamme d'estimations qu'ils pouvaient faire. Autrement dit, ils se rapprochaient de la vérité. En 2019, pour le plaisir du monde des mathématiques, Verstraete et Mubayi ont utilisé des graphiques pseudorandom pour résoudre r(3,t). Cependant, Verstraete a eu du mal à construire un graphique pseudorandom qui pourrait aider à résoudre r(4,t). Il a commencé à tirer dans différents domaines des mathématiques en dehors de la combinatoire, y compris la géométrie finie, l'algèbre et la probabilité. Finalement, il s'est joint à Mattheus, un boursier postdoctoral de son groupe dont les origines étaient en géométrie finie. Une fois qu'ils ont eu le graphique pseudorandom en place, ils ont quand même dû décrocher plusieurs morceaux de mathématiques. Cela a pris presque un an, mais finalement ils ont réalisé qu'ils avaient une solution : r(4,t) est proche d'une fonction cubique de t. Si vous voulez une fête où il y aura toujours quatre personnes qui se connaissent tous ou des gens qui ne se connaissent pas tous, vous aurez besoin d'environ t3 personnes présentes. Il y a un petit astérisque (en fait un o) parce que, rappelez-vous, c'est une estimation, pas une réponse exacte. Mais t3 est très proche de la réponse exacte. ⁣https://phys.org/news/2023-10-....math-problem-century

Des chercheurs ont utilisé l'IA pour concevoir un « tableau périodique des formes géométriques ». Comme le tableau périodique des éléments a révolutionné la chimie, il pourrait transformer notre compréhension des formes géométriques. ⁣https://trustmyscience.com/tab....leau-periodique-form

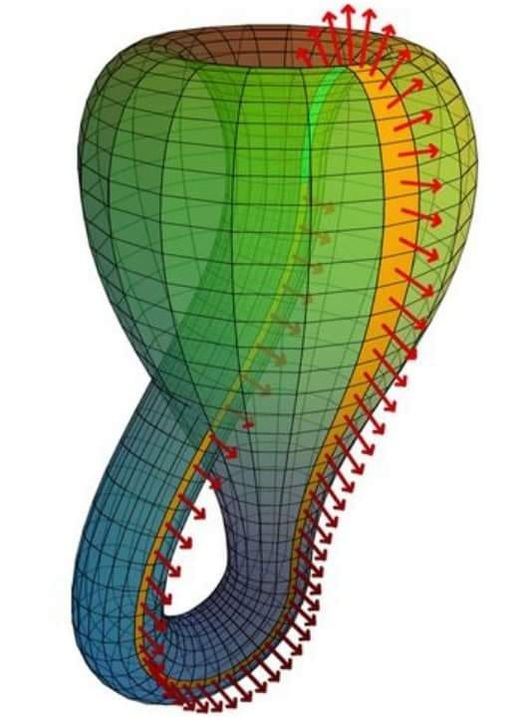
⁣ Bouteille Klein : 4ème objet dimensionnel sans frontière ! Si une fourmi devait marcher le long de cette ligne de bande jaune, elle ne traverserait jamais un bord pour aller à l'intérieur, et elle marcherait pour toujours ou continuellement. C'est parce que la bouteille Klein, un objet de 4ème dimension, n'a qu'un côté, ou on pourrait dire qu'elle n'a pas de limite. Vous remarquerez qu'il y a un point d'auto-intersection mais cela peut être expliqué par les mathématiciens lorsque la bouteille Klein est vue en 3 dimensions, se forme lorsque les bords de 2 bandes mobius sont réunis. Sur la base de son analogue en 3 dimensions appelé la bande de Mobius qui a une limite, il a été observé par son inventeur allemand Félix Klein en 1882.

⁣Les mathématiques ont enfin leur musée ! La Maison Poincaré, projet porté par le hashtag#cnrs et Sorbonne Université, permettra au grand public de découvrir de manière ludique et interactive les maths et leurs applications. Dans ce haut lieu de l'histoire des sciences rénové, les visiteurs vont pouvoir explorer les maths dans tous leurs états : concepts, applications, interactions avec d’autres disciplines scientifiques ou artistiques. Le tout en restant connecté à la recherche, en proposant des résidences d’artistes et des conférences. 📅 à partir du 30 septembre 2023 📍 11, rue Pierre et Marie Curie à Paris (5e arr.) ⁣https://lejournal.cnrs.fr/arti....cles/a-la-maison-poi

⁣Des chercheurs révèlent une connexion surprenante entre la théorie des nombres et la génétique évolutive, notamment des motifs mathématiques qui influenceraient la biologie.⁣ https://trustmyscience.com/mat....hematiques-pures-ins

⁣Les nombres imaginaires sont apparus dès la première moitié du XVIe siècle. La physique y a rapidement vu de précieux outils mathématiques fondamentaux. La mécanique quantique leur attribue un rôle essentiel, comme nous l’explique le mathématicien et philosophe Frédéric Patras. ⁣https://www.pourlascience.fr/s....d/mathematiques/la-t

⁣De nouveaux codes puissants correcteurs d'erreurs quantiques pourraient aider à accélérer l'arrivée d'ordinateurs quantiques utiles. ⁣https://www.quantamagazine.org..../new-codes-could-mak

⁣De nouveaux codes puissants correcteurs d'erreurs quantiques pourraient aider à accélérer l'arrivée d'ordinateurs quantiques utiles. ⁣https://www.quantamagazine.org..../new-codes-could-mak

⁣ Les mathématiques peuvent, d'une part, être considérées comme une lentille incroyable à travers laquelle on peut voir le monde ; une connaissance importante à la disposition de tous, qui favorise les jeunes habilités prêts à penser quantitativement à leur travail et à leur vie et qui est équitablement accessible à tous les étudiants grâce à leurs études et à leurs études travail dur. D'un autre côté, les mathématiques peuvent être considérées comme un sujet qui sépare les enfants en ceux qui le peuvent et ceux qui ne le peuvent pas, et cela est précieux comme un mécanisme de tri, permettant aux gens de qualifier certains enfants comme intelligents et d'autres comme non intelligents. — Jo Boaler, mentalités mathématiques.

⁣À l’issue de 1 500 heures de calculs, des mathématiciens sont parvenus à déterminer ce nombre qui résistait depuis plus de trente ans. ⁣286 386 577 668 298 411 128 469 151 667 598 498 812 366. Il ne s’agit pas d’une juxtaposition de 42 chiffres pris au hasard. Cette quantité correspond au nombre de fonctions booléennes monotones en neuf dimensions. Et c’est au terme de plusieurs années de travail et de 1 500 heures de calculs que Lennart Van Hirtum, informaticien à l’université de Paderborn, en Allemagne, Patrick De Causmaecker, de KU Leuven, en Belgique, et leurs collègues l’ont récemment déterminé. Le calcul de ce « neuvième nombre de Dedekind » complète la suite des nombres de Dedekind connus à ce jour (référencée A000372 sur l’encyclopédie en ligne des suites, OEIS). ⁣https://www.pourlascience.fr/s....d/mathematiques/le-n

⁣L'épitome de la beauté : 10 concepts exquis qui définissent la physique moderne... https://thenerdszone.medium.co....m/the-epitome-of-bea

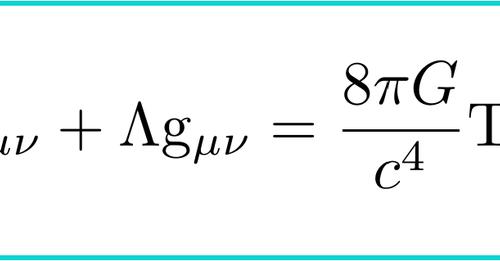
⁣La mécanique quantique nous montre que la même expérience, répétée à plusieurs reprises dans les mêmes conditions, peut donner des résultats différents. ⁣https://bigthink.com/13-8/quan....tum-superposition/#E

⁣Dériving de l'identité d'Euler à l'aide de la série Maclaurin ⁣https://medium.com/@2305sakake..../deriving-eulers-ide

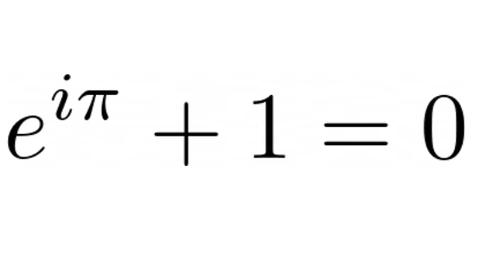
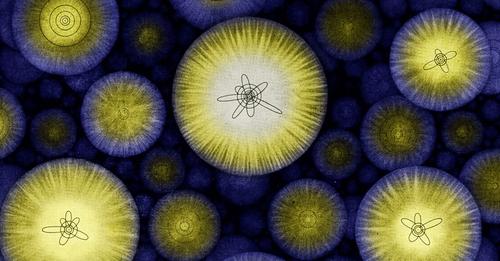
⁣⁣Les nombres imaginaires semblent être tissés dans la mécanique quantique. (à partir de 2021) https://www.sciencenews.org/ar....ticle/quantum-physic

⁣Enjoy learning mathematics. ⁣https://mathematicsart.com/

⁣Calculate the following limit, if it exist. ⁣https://mathematicsart.com/sol....ved-exercises/soluti

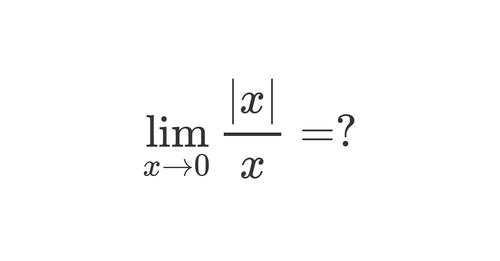
⁣Depuis leur découverte dans les années 1830, les groupes sont devenus l'un des objets les plus importants en mathématiques. La théorie de la représentation aide les mathématiciens à convertir le monde parfois mystérieux des groupes en un territoire bien traîné de l'algèbre linéaire. (à partir de 2020) ⁣https://www.quantamagazine.org..../the-useless-perspec

⁣Des chercheurs ont développé une approche utilisant un « spin quantique central » pour simplifier les calculs quantiques, permettant une diminution des erreurs, une vitesse accrue ainsi qu'une meilleure compatibilité avec divers algorithmes clés. ⁣https://trustmyscience.com/inf....ormatique-quantique-

⁣ARTE. Film documentaire « L’Odyssée des chiffres ». Aujourd’hui, arrivée à Béjaia de l’équipe de tournage (conduite par le réalisateur Benoit Laborde). Après la Chine, l’Inde, l’Italie et Baghdad, c’est le tour de l’histoire des « Huruf Al-Ghubari » (les chiffres arabes) et de leur popularisation en Europe par le Célèbre mathématicien italien Léonardo Fibonacci (vers 1180). Ici, accueil au niveau du CDHB/Gehimab, sis à la BPLP Aamriw. ⁣https://www.facebook.com/profi....le.php?id=1000578657

⁣Plus tôt cet été, les étudiants de l'Université du Colorado, Boulder ont découvert un problème avec la conjecture locale-mondiale, une prédiction sur les emballages de cercle que de nombreux théoriciens des nombres avaient considéré comme étant tout sauf prouvé. ⁣https://www.quantamagazine.org..../two-students-unrave

⁣Les mathématiques grecques, l'étude des nombres et de leurs propriétés, des modèles, de la structure, de l'espace, des changements apparents et des mesures, auraient été créées par Thalès de Milet (vers 585 av. J.-C.), mais avaient été clairement comprises pendant les périodes de la civilisation minoenne (2000-1450 av. J.-C.) et de la civilisation mycénienne (vers 1700-1100 av. J.-C.) et étaient dérivées de systèmes mathématiques mésopotamiens et égyptiens plus anciens. ⁣https://www.worldhistory.org/t....rans/fr/2-606/mathem

⁣Magnifique. "Les ⁣mathématiques c'est pas le sujet le simple à aborder. La beauté quand à elle, c'est une notion subjectif, extrêmement subjectif. De plus l'association beauté et mathématiques ne sera pas évidentes pour la plupart du commun des mortels qui regarderont cette vidéo. Comment exprimer la beauté d'une discipline aussi flou et abstraite que les mathématiques ?"

⁣Le dernier numéro de Mathématiques du calcul, volume 92, numéro 342, est maintenant disponible sur : http://ow.ly/mZmV50NGiX4

"La sagesse et la fille de l'expérience". ⁣ Léonard de Vinci.

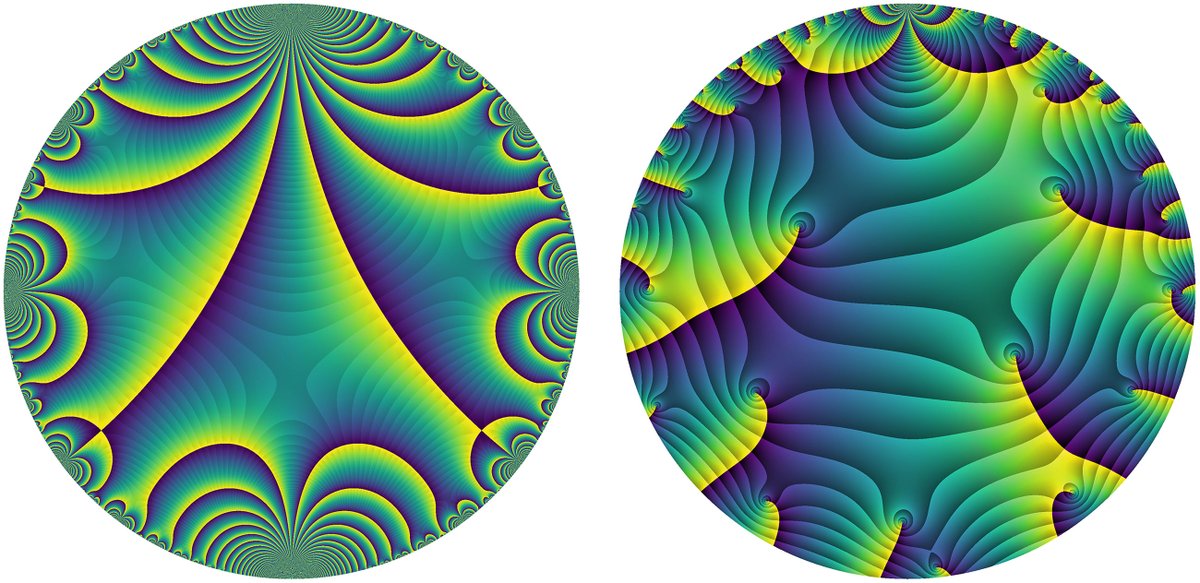
⁣Les formes modulaires de congruence (à gauche) ont une structure supplémentaire dont les formes modulaires de non-congruence (à droite) manquent. Les formes modulaires de congruence se sont avérées utiles dans un large éventail de problèmes, tandis que les formes modulaires de non congruence ont été plus difficiles à étudier. https://www.quantamagazine.org..../long-sought-math-pr

⁣https://mathigon.org/timeline

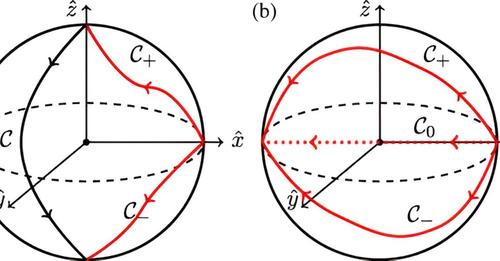
⁣Cette équation est souvent décrite comme la plus belle de toutes les mathématiques. Chacun de ses nombres, 0, 1, π, i et e symbolise toute une branche de mathématiques, et de cette façon l'équation peut être vue comme une confluence glorieuse, un témoignage de l'unité des mathématiques. https://www.quantamagazine.org..../how-infinite-series

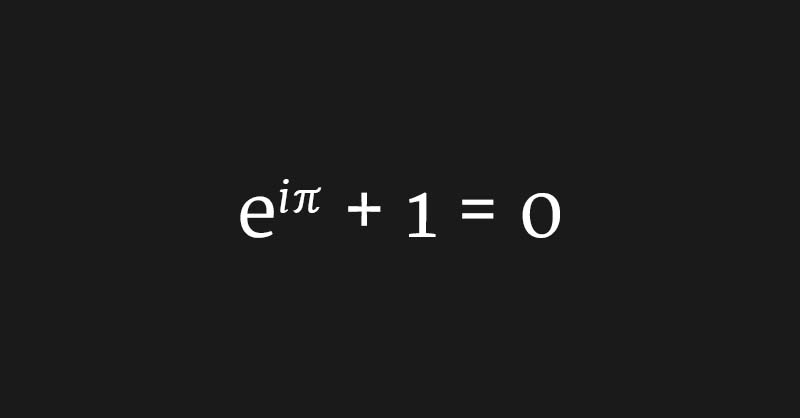
⁣« Francis Bonahon a passé en revue les œuvres collectées de William P. Thurston » dans l'édition d'avril des avis de l'AMS. « C'est un grand hommage au génie de l'un des plus grands mathématiciens de tous les temps, ainsi qu'une grande ressource pour les mathématicien d'aujourd'hui et de demain. ” Lire la critique complète : http://ow.ly/McTH50NsOYg

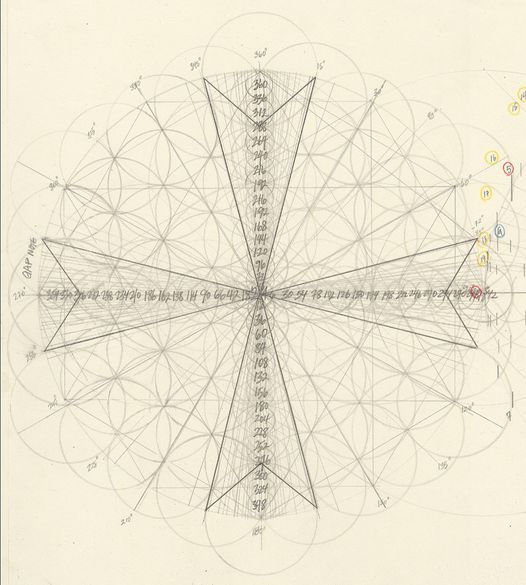
⁣ Une autre trouvaille et réalisation ! L'arbre de vie « étendu » crée les lignes de rapport d'or ( φ) du cube de Metatron, dont toute géométrie émerge. Les lignes φ Metatron (36° et 72°) sont fondamentales à l'hyperdimensionnel et à la perspective multidimensionnelle que l'on peut trouver et utiliser dans le cube de Metatron, (que DaVinci aurait beaucoup travaillé avec cette géométrie particulièrement). La fusion du Pentagone et de l'Hexagone ; la convergence du rationnel et de l'irrationnel. L'art rencontre la science ; le cerveau gauche et le cerveau droit. ACCEPTER la polarité, c'est la TRANSCENDRE. Le Pentagone apporte l'élément émotionnel et créatif au mariage des 5 et des 6. La géométrie est si belle et incroyable... workuvre d'art par RG. ⁣https://robertedwardgrant.com/....the-extended-tree-of