Un article de recherche récemment publié propose une “loi d’augmentation de l’information fonctionnelle” dans le but de codifier le comportement universellement observé des systèmes évoluant naturellement – des étoiles et des planètes aux organismes biologiques – qui augmentent leur complexité fonctionnelle au fil du temps.
Pour codifier ce comportement, il est proposé que l’information fonctionnelle d’un système augmente (c’est-à-dire que le système évolue) si de nombreuses configurations différentes du système sont sélectionnées pour une ou plusieurs fonctions.
Il convient de noter que le terme “évolution” est utilisé dans un sens général, car l’évolution darwinienne est considérée comme spécifique au système biologique et nécessite un matériel héréditaire ou une forme de mémoire transmissible et stable d’une variante itérative à la suivante, ce qui n’est traditionnellement pas considéré comme opérationnel dans les systèmes physiques dynamiques génériques, bien que des théories telles que le réseau unifié de mémoire spatiale et la résonance morphique puissent étendre le cas particulier de l’évolution darwinienne aux systèmes physiques dynamiques en général, car elles supposent un support de mémoire transmissible via la mémoire spatiale ou un champ morphogénique, respectivement.
Un “système évolutif” est défini comme un phénomène collectif composé de nombreux éléments en interaction qui présente une augmentation temporelle de la diversité, de la distribution et du comportement structuré. En tant que tels, les systèmes évolutifs sont un aspect omniprésent du monde naturel, apparaissant dans de nombreux contextes naturels à de nombreuses échelles spatiales et temporelles.
Bien qu’il ne s’agisse pas de la première étude de ce type à proposer un mécanisme universel pour expliquer la tendance observable quasi omniprésente des divers systèmes naturels à évoluer vers des niveaux de complexité de plus en plus élevés – et de manière exceptionnelle, vers une complexité fonctionnelle -, une codification rigoureuse approchant le niveau d’une “loi naturelle” – comme les lois du mouvement, de la gravité ou de la thermodynamique – est significative.
Dans notre étude The Unified Spacememory Network, nous avons proposé une telle loi selon laquelle les systèmes naturels génériques évolueront vers des niveaux toujours plus élevés d’organisation synergique et de complexité fonctionnelle. Dans l’approche du réseau unifié de mémoire spatiale, les niveaux toujours plus élevés d’informations fonctionnelles des systèmes évoluant naturellement sont en partie fonction des propriétés de mémoire de l’espace.
Dans l’étude récente, les chercheurs utilisent une analyse comparative des équivalences entre les systèmes évoluant naturellement – y compris, mais sans s’y limiter, la vie – pour identifier d’autres caractéristiques de cette “loi manquante” de la complexité fonctionnelle croissante, comme l’observation que tous les systèmes évolutifs sont composés de divers éléments qui peuvent se combiner dans des états configurationnels qui sont ensuite sélectionnés pour ou contre sur la base de la fonction, et au fur et à mesure que l’espace de phase configurationnel (souvent très vaste) est exploré, les combinaisons qui sont maximalement fonctionnelles seront préférentiellement sélectionnées.
L’étude propose également des mécanismes relevant de la loi de l’augmentation de l’information fonctionnelle qui expliquent la tendance des systèmes évolutifs à augmenter leur diversité et à générer de la nouveauté.
1. Universalité des systèmes évolutifs :
Cette certitude est telle que nous pouvons affirmer avec audace qu’il est absurde pour les êtres humains de tenter de le faire, ou d’espérer qu’un jour, un autre Newton pourra nous expliquer, en termes de lois naturelles non ordonnées par l’intention, comment même un simple brin d’herbe est produit.
Kant, Critique du jugement (1790)
L’univers regorge de systèmes complexes en évolution – l’univers lui-même peut être considéré comme un système en évolution (figure 1) – et l’un des principaux objectifs de la science unifiée est de comprendre et de codifier la dynamique sous-jacente qui génère les systèmes en évolution et la complexification qui en résulte, qu’il s’agisse de l’émergence spontanée dans les systèmes auto-organisés ou de mécanismes d’ordonnancement sous-jacents définissables qui se rapprochent des “lois de la nature” opérationnelles. Des études telles que A unifying concept for Astrobiology de E.J. Chaisson, qui définit quantitativement les systèmes évolutifs sur la base du flux d’énergie, de sorte que tous les systèmes ordonnés – des planètes rocheuses et des étoiles brillantes aux abeilles bourdonnantes et aux séquoias – peuvent être jugés empiriquement et uniformément en mesurant la quantité d’énergie acquise, stockée et exprimée par ces systèmes [1], Du modèle universel du biophysicien Antonis Mistriotis décrivant la structure et les fonctions des systèmes vivants [2], dans lequel les systèmes évolutifs comme la vie sont identifiés comme un “phénomène thermodynamique loin de l’équilibre qui implique la création d’un ordre (réduction de l’entropie interne) par l’accumulation et le traitement de l’information”, il existe une base solide dans ce domaine de recherche pour comprendre la physique de la vie et des systèmes évolutifs complexes en général.
Une question ouverte pour comprendre la complexification de la matière dans le temps est de savoir s’il existe des lois naturelles – semblables à la codification des moyennes statistiques en tant que lois sous-jacentes à la thermodynamique – qui sont opérationnelles dans les systèmes dynamiques complexes génériques qui peuvent être caractérisés comme ayant une évolution asymétrique dans le temps. Chaisson définit la complexité comme suit : “un état d’intrication, de complication, de variété ou d’implication, comme dans les parties interconnectées d’un système – la qualité d’avoir de nombreux composants différents en interaction” et note que “l’augmentation potentiellement spectaculaire de la complexité au cours du dernier demi-milliard d’années depuis la fin de la période précambrienne sur Terre est particulièrement intrigante. S’apparentant peut-être à une forme moderne de platonisme, un principe sous-jacent, une loi unificatrice ou un processus continu crée des ordres et maintient toutes les structures de l’Univers, ce qui nous permet d’étudier tous ces systèmes sur un terrain uniforme et plat” [1, p. 93].
Figure 1. Flèche stylisée du temps mettant en évidence les principales caractéristiques de l’histoire cosmique en termes de processus évolutif. Depuis ses origines supposées à haute énergie, il y a environ 14 ans (à gauche), jusqu’à l’ici et maintenant (à droite), avec des systèmes complexes en évolution donnant naissance à la culture, à la cybernétique et à l’intelligence artificielle. Les principales phases de l’évolution qui ont produit, à leur tour, des quantités croissantes d’ordre et de complexité dans tous les systèmes matériels sont indiquées en diagonale dans la partie supérieure : évolution particulaire, galactique, stellaire, planétaire, chimique, biologique et culturelle. L’évolution cosmique englobe toutes ces phases. Image et description de l’image de Chaisson [1].
Aujourd’hui, la recherche sur la nature des systèmes évolutifs complexes a fait de nouveaux progrès. Une étude récemment publiée, intitulée On the Roles of Function and Selection in Evolving Systems (Les rôles de la fonction et de la sélection dans les systèmes évolutifs), par Wong et al. explique comment les lois physiques macroscopiques existantes (tableau 1) ne semblent pas décrire correctement ces systèmes (évolutifs complexes) [3]. Historiquement, il a été généralement accepté qu’il n’y a pas de loi universelle équivalente opérationnelle dans le développement et l’évolution des systèmes dynamiques décrivant une tendance à l’augmentation de la complexité fonctionnelle parce qu’il est supposé que la dynamique sous-jacente est intrinsèquement stochastique (déterminée de manière aléatoire ; ayant une distribution de probabilité aléatoire ou un modèle qui peut être analysé statistiquement mais ne peut être prédit avec précision) et que, par conséquent, tout processus général de développement ou de complexification se déroule par le biais d’un accident aléatoire après l’autre sans directionnalité naturelle sous-jacente, processus d’ordonnancement ou mécanisme qui équivaudrait à une loi physique à partir de laquelle, par exemple, un résultat de probabilité presque précis pourrait être calculé pour le comportement et la trajectoire de tout système évolutif donné, à la limite que certains systèmes dynamiques complexes sont symétriques dans le temps et non déterministes (voir, par exemple, la réaction de Belousov-Zhabotinsky).
Ainsi, dans des études telles que The Astrobiological Copernican Weak and Strong Limits for Intelligent Life [4], de Westby et Conselice, qui utilisent des données pour calculer la prévalence de la vie intelligente dans la Voie lactée, les chercheurs doivent recourir à une analyse probabiliste qui tient compte d’un éventail de possibilités allant d’un “scénario fort” avec des hypothèses strictes sur l’improbabilité de l’évolution de la matière en organismes vivants sur une exoplanète habitable donnée à un “scénario ultrafaible” plus permissif dans les hypothèses sous-jacentes [tableau 2]. Ainsi, par exemple, dans le cadre des hypothèses les plus permissives (ultrafaibles), ils calculent une prévalence d’environ 4. 63 X 1010 (~40 milliards) d’occurrences de vie primitive se développant sur des planètes de notre galaxie, alors que dans le cadre des hypothèses les plus strictes (fortes), ils estiment qu’il devrait y avoir au moins 36 civilisations intelligentes (communicantes) dans notre galaxie. Si toutefois les restrictions sont assouplies et que les calculs sont effectués en partant de l’hypothèse que la vie a une probabilité relativement décente de se développer sur des planètes rocheuses où il y a de l’eau liquide et une source d’énergie constante à faible entropie, le nombre de civilisations intelligentes potentielles dans notre galaxie est alors exponentiellement plus élevé que 36.

S’il existait des lois macrophysiques connues définissant le comportement des systèmes évolutifs, les chercheurs Wesby et Conselice n’auraient pas besoin de s’appuyer sur des “hypothèses” pour leur analyse. Outre la capitulation apparemment non scientifique qui consiste à attribuer le développement de systèmes évolutifs génériques – pas seulement la vie – au hasard, qui prévaut dans le monde universitaire conventionnel, ou à s’appuyer sur un comportement d’ordonnancement purement émergent qui peut se manifester spontanément dans les systèmes auto-organisés [voir Kauffman, 5], cette vision orthodoxe semble négliger des observables importants tels que l’augmentation uniforme de la complexité et de la diversité de la matière qui est évidente au cours de l’histoire de l’univers et l’exemple remarquable de la matière qui s’organise en un système superlatif fonctionnellement complexe qu’est l’organisme vivant. En effet, la prédominance de l’hypothèse selon laquelle le hasard est fondamental et l’émergence de l’ordre n’est plus rationnellement attribuée qu’à des coïncidences ou à des accidents fortuits conduit les théoriciens à postuler qu’il est extrêmement improbable que quelque chose comme la biogenèse se produise, en dépit de l’observation plus générale selon laquelle les systèmes matériels dans l’espace et le temps ont une tendance inexorable à la complexification et à l’organisation fonctionnelle synergique.
Par exemple, Andrew Watson, dans Implications of an Anthropic Model of Evolution for Emergence of Complex Life and Intelligence [6], déduit qu’il n’y a que 2,6 % de chances que l’une des transitions majeures dans l’évolution des systèmes primordiaux de réplication moléculaire se transforme en cellules vivantes (tableau 3), ce qui suggère qu’il est très improbable que les circonstances permettent la biogenèse dans des délais similaires à la durée de vie connue de la biosphère terrestre (ce qui soutient l’hypothèse de la “Terre rare”). Cependant, si nous prenons en considération l’infodynamique opérant à partir d’un champ directeur, comme le code quantique informationnel de Meijer et al [7], la résonance morphique de Sheldrake [8], ou le concept d’info-entropie holomorphe de Chris Jeynes et Michael Parker [9], nous pouvons en déduire rationnellement que la dynamique organisationnelle, qui se rapproche d’une véritable entropie effective, est en train de se développer, qui se rapproche d’une véritable force entropique effective ou d’une loi physique de la complexité, conduira les systèmes à une organisation fonctionnelle de plus en plus poussée et la biogenèse sera un résultat relativement probable et universel partout où les conditions sont favorables à l’habitabilité biologique.

Cette hypothèse de l’approche orthodoxe est toutefois en train de changer, même dans les cercles conventionnels. En évaluant l’augmentation uniforme de la complexité et de la fonctionnalité des systèmes physiques dans l’univers, Wong et al. ont dérivé une loi physique qui, selon eux, sous-tend le comportement des systèmes évolutifs, selon laquelle l’information fonctionnelle d’un système augmentera (c’est-à-dire que le système évoluera) si de nombreuses configurations différentes du système font l’objet d’une sélection pour une ou plusieurs fonctions. En identifiant des équivalences conceptuelles entre des phénomènes disparates – un processus qui a été à la base de l’élaboration des lois de la nature précédentes, comme celles du tableau 1 – l’équipe de recherche prétend identifier une “loi manquante” potentielle. Elle postule que les systèmes en évolution – y compris, mais sans s’y limiter, l’organisme vivant – sont composés de divers éléments qui peuvent se combiner dans des états de configuration qui sont ensuite sélectionnés pour ou contre sur la base de la fonction. Ainsi, par le biais d’une délimitation des sources fondamentales de sélection : (1) sélection statique, (2) persistance dynamique et (3) génération de nouveauté, Wong et al. ont proposé une loi asymétrique dans le temps qui stipule que l’information fonctionnelle d’un système augmentera au fil du temps lorsqu’il est soumis à une sélection pour une ou plusieurs fonctions.
2. La loi de l’information fonctionnelle croissante :
Les lois présentées dans le tableau 1 figurent parmi les déclarations les plus importantes sur le comportement fondamental des systèmes physiques que les scientifiques ont découvertes et formulées à ce jour. Pourtant, comme le soulignent Wong et al. dans leur récente étude, la loi de complexité croissante brille par son absence. La nature regorge d’exemples de systèmes complexes et l’évolution de systèmes variés, y compris les étoiles, les minéraux, les atmosphères et la vie, est une merveille omniprésente dans le monde naturel (figure 2). L’étude On the Roles of Function and Selection in Evolving Systems (Les rôles de la fonction et de la sélection dans les systèmes évolutifs) définit au moins trois attributs définitifs des systèmes évolutifs qui semblent conceptuellement équivalents : 1) ils se forment à partir de nombreux composants qui ont le potentiel d’adopter un grand nombre de configurations différentes sur le plan combinatoire ; 2) il existe des processus qui génèrent de nombreuses configurations différentes ; et 3) les configurations sont préférentiellement sélectionnées sur la base de la fonction. Les mécanismes universels de sélection et de génération de nouveauté – décrits ci-dessous – poussent ces systèmes à évoluer par l’échange d’informations avec l’environnement et, par conséquent, l’information fonctionnelle et la complexité d’un système augmenteront si de nombreuses configurations différentes du système sont sélectionnées pour une ou plusieurs fonctions.

Figure 2. L’histoire de la nature, du Big Bang à nos jours, est représentée graphiquement sous la forme d’une spirale avec des événements notables annotés. Chaque milliard d’années (Ga) est représenté par un angle de 90 degrés de la spirale. Les 500 derniers millions d’années sont représentés par une section à 90 degrés pour plus de détails sur notre histoire récente. Parmi les événements représentés figurent l’émergence des structures cosmiques (étoiles, galaxies, planètes, amas et autres structures), l’émergence du système solaire, de la Terre et de la Lune, les événements géologiques importants (gaz dans l’atmosphère, grandes orogénies, périodes glaciaires, etc.) et l’émergence et l’évolution des êtres vivants (premiers microbes, plantes, champignons, animaux, espèces d’hominidés).
3. Origine de la sélection et de la fonction :
Examinons maintenant de plus près les trois attributs identifiés et délimités par Wong et al. dans leur étude ; les trois attributs définitifs des systèmes évolutifs sont : (1) la sélection statique, identifiée comme le principe de la persistance statique ; (2) la persistance dynamique, identifiée comme le principe de la persistance des processus ; et (3) la génération de nouveauté, un principe de sélection pour la nouveauté.
Principe de persistance statique (sélection de premier ordre) : les configurations de la matière ont tendance à persister à moins qu’il n’existe des voies cinétiquement favorables à leur incorporation dans des configurations plus stables. Comme le décrivent Wong et al., la persistance fournit non seulement une énorme diversité de composants, mais “elle fournit également des “batteries d’énergie libre” ou des “poches de néguentropie” dans tout l’univers qui alimentent des entités dynamiques persistantes”.
L’équipe de recherche a dérivé le paramètre de sélection de premier ordre de la loi de la complexité croissante en imaginant un univers alternatif qui commence comme le nôtre mais qui ne produit finalement aucun système de complexité croissante. Comme décrit, “dans un tel monde sans modèle, les systèmes progressent doucement vers des états d’entropie plus élevée sans générer de poches durables de faible entropie ou de “poches de néguentropie”, par exemple, en raison de l’absence de forces d’attraction (gravité, électrostatique)” ou de constantes comme alpha qui ne sont pas “finement réglées” et des atomes stables qui ne peuvent même pas se former. Dans notre étude The Unified Spacememory Netwok [10], nous avons suivi une expérience de pensée similaire pour illustrer le mécanisme d’organisation synergique croissante et de complexité fonctionnelle via l’attribut mémoire du manifold spatio-temporel à connexions multiples et l’architecture de connectivité neuromorphique de type ER=EPR du Spacememory Network (Figure 3).
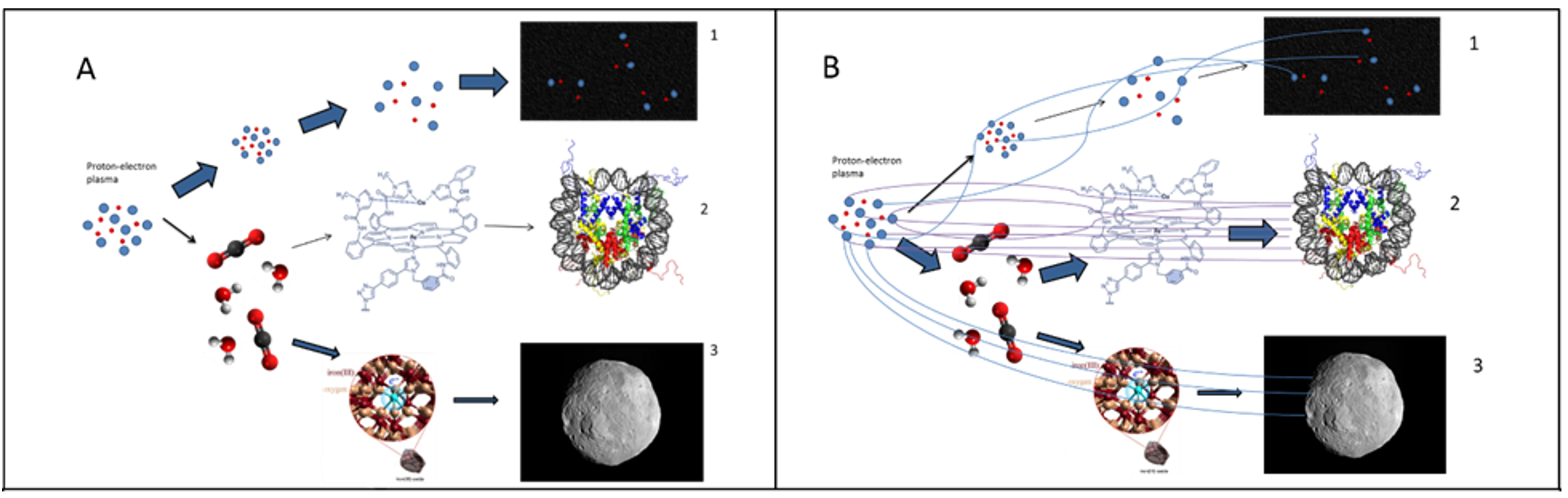
Figure 3 (A) Chemins potentiels de l’évolution de la matière dans l’Univers (à titre d’illustration conceptuelle uniquement). Les flèches indiquent le degré relatif de probabilité selon les modèles conventionnels, le chemin potentiel 1 ayant le degré de probabilité le plus élevé, mais le degré d’ordre et de complexité le plus faible ; le chemin potentiel 2 ayant le degré de probabilité le plus faible, mais le degré d’ordre et de complexité le plus élevé ; et le chemin potentiel 3 ayant une valeur d’espérance probabiliste médiane. (B) Effet postulé des interactions non locales (corrélations EPR) du réseau d’information du micro-vortex ERb=EPR sur le développement et l’évolution des structures atomiques et moléculaires dans l’univers. Les connexions à haute densité du micro-vortex ERb=EPR, qui font partie intégrante des molécules complexes et hautement ordonnées (voie 2), produisent une interaction plus forte à travers la dimension temporelle, ainsi qu’au niveau intramoléculaire. Cela influence l’interactivité des atomes de telle sorte qu’une véritable force pousse les systèmes à former des associations complexes – un effet néguentropique. L’échange d’informations trans-temporelles, qui apparaît comme un attribut de mémoire de l’espace, est un effet d’ordonnancement qui pousse la matière dans l’univers à des niveaux plus élevés d’organisation synergique et de complexité fonctionnelle.
À l’instar de notre conclusion dans The Unified Spacmemory Network, Wong et al. concluent que les états de la matière dans notre univers n’évoluent pas sans heurt vers une entropie maximale (voie 1 de la figure 3), mais qu’il existe au contraire des forces néguentropiques qui “contrarient” la dissipation de l’énergie libre “permettant l’existence durable de déséquilibres” et aboutissant à des “poches de néguentropie” qui alimentent des entités dynamiquement persistantes (voie 2 de la figure 3).
L’importance de la propriété de certains états de la matière de diminuer l’entropie, de maintenir et de perpétuer des états thermodynamiques loin de l’équilibre dans le cadre de la complexification des systèmes évolutifs, menant à l’organisme vivant, a été soulignée dans des études antérieures telles que le travail de l’auteur sur la définition de la transition clé de la matière abiotique à la matière biotique organisée [11]. Mistriotis a encore élucidé le mécanisme de l’action néguentropique des systèmes vivants comme impliquant le traitement de l’information, par lequel les opérations logiques, comme celles d’un circuit électronique, diminuent l’entropie interne d’un système évolutif complexe comme l’organisme vivant et, par conséquent, tous les systèmes vivants effectuent nécessairement des opérations logiques similaires aux circuits électroniques. La logique est nécessaire dans le système vivant pour exécuter les fonctions auto-similaires de diminution de l’entropie dans l’organisation hiérarchique de l’organisme, de sorte que la similitude avec le traitement de l’information d’un circuit électronique est encore plus poussée pour établir des similitudes avec la fonctionnalité de lecture-écriture de la mémoire d’un ordinateur, ce qui montre que les systèmes évolutifs complexes comme la vie traitent l’information à un niveau complexe [12].
Sélection de second ordre, persistance des processus – ce deuxième postulat définit la caractérisation de la “fonction” qui peut être attribuée à un processus et la manière dont la fonctionnalité est finalement sélectionnée par opposition aux processus qui ne contribuent pas à l’efficacité causale sur les états internes d’un système. Comme le décrivent Wong et al, “dans la mesure où les processus ont une efficacité causale sur l’état interne d’un système ou sur son environnement externe, ils peuvent être qualifiés de fonctions. Si une fonction favorise la persistance du système, elle sera sélectionnée”.
Sélection de troisième ordre pour la nouveauté – le paramètre de sélection de troisième ordre répond à un défi important de la théorie de l’évolution, dans laquelle la sélection naturelle peut décrire la sélection et la préservation des phénotypes adaptatifs mais ne peut pas expliquer la génération de novo de la nouveauté [13]. La nouvelle étude aborde ce problème en avançant qu'”il existe des pressions favorisant les systèmes qui peuvent inventer de nouvelles fonctions de manière illimitée, c’est-à-dire des pressions de sélection pour la génération de nouveauté”. L’ajout de nouvelles fonctions qui favorisent la persistance des fonctions principales augmente essentiellement la “barrière cinétique” d’un système dynamique contre la décroissance vers l’équilibre. La nouvelle étude donne plus de détails : “un système capable d’explorer de nouvelles portions de l’espace des phases peut être en mesure d’accéder à de nouvelles sources d’énergie libre qui contribueront à maintenir le système hors de l’équilibre ou à l’en éloigner encore davantage. En général, dans un univers qui offre un vaste espace de possibilités d’une grande richesse combinatoire, la découverte de nouvelles configurations fonctionnelles est sélectionnée lorsqu’il existe un nombre considérable de configurations fonctionnelles qui n’ont pas encore fait l’objet d’une sélection.
À l’instar de la cognition sans échelle et de l’organisation complexe des intelligences composées de Mike Levin [14], Wong et al. soulignent de manière plus générale que les systèmes les plus compliqués sont des réseaux imbriqués de systèmes complexes plus petits, chacun persistant et contribuant à maintenir la persistance de l’ensemble. Il est important de noter que dans les systèmes complexes imbriqués, des fonctions auxiliaires peuvent apparaître, comme les tourbillons qui se détachent d’un champ d’écoulement primaire.
Les paramètres de sélection pour la fonction de premier, deuxième et troisième ordre sont proposés pour expliquer les origines de la sélection et de la fonction, étant donné que l’univers que nous observons génère constamment certaines structures ordonnées et certains systèmes structurés dont l’existence et l’évolution dans le temps ne peuvent être expliquées de manière adéquate par les lois de la nature identifiées jusqu’à présent, telles que celles résumées dans le tableau 1. Ces postulats conduisent à la formalisation d’une sorte de loi décrivant l’augmentation de la complexité des systèmes par l’existence de pressions de sélection :
Les systèmes composés de nombreux agents en interaction présentent une augmentation de la diversité, de la distribution et/ou du comportement structuré lorsque de nombreuses configurations du système sont soumises à des pressions sélectives.
Il existe donc une base universelle pour la sélection et un formalisme quantitatif ancré dans le transfert d’informations entre un système en évolution et son environnement.
4. Information fonctionnelle et évolution des systèmes :
Toutes les lois naturelles du tableau 1 impliquent un paramètre quantitatif tel que la masse, l’énergie, la force ou l’accélération, ce qui soulève naturellement la question suivante : “Existe-t-il un paramètre équivalent associé aux systèmes en évolution ?” L’étude la plus récente montre que c’est effectivement le cas, et que la réponse est l’information (mesurée en bits), en particulier l'”information fonctionnelle”, telle qu’elle a été introduite dans des études comme Functional Information and the Emergence of Biocomplexity (Information fonctionnelle et émergence de la biocomplexité) [15]. L’information fonctionnelle quantifie l’état d’un système qui peut adopter de nombreuses configurations différentes en termes d’information nécessaire pour atteindre un “degré de fonction” spécifié, où la “fonction” peut être aussi générale que la stabilité par rapport à d’autres états ou aussi spécifique que l’efficacité d’une réaction enzymatique particulière.
En ce qui concerne la loi de l’augmentation de l’information fonctionnelle pour les systèmes génériques évolutifs, le formalisme de l’information fonctionnelle met en évidence une caractéristique universelle importante :
L’information fonctionnelle d’un système augmentera (c’est-à-dire que le système évoluera) si de nombreuses configurations différentes du système sont soumises à une sélection pour une ou plusieurs fonctions.
Comme le décrivent Wong et al., ce postulat est un parallèle étroit avec la loi de complexité croissante proposée précédemment, qui stipule que la sélection naturelle, agissant seule, tend à accroître la complexité d’un système [17]. Il est intéressant d’examiner le lien mécanique entre ce postulat et la physique holographique, selon laquelle une augmentation de l’information et, d’après cette étude, la complexification correspondante du système seront corrélées à l’augmentation des hypersurfaces spatio-temporelles, l’information étant codée sur la surface de l’espace-temps sous forme de mémoire spatiale. Les circuits de connectivité de ces hypersurfaces spatio-temporelles, connus sous le nom de ponts d’Einstein-Rosen, peuvent expliquer mécaniquement l’augmentation de la complexité fonctionnelle, en dehors des seules pressions de sélection, et l’augmentation correspondante de l’organisation synergique des systèmes fonctionnels complexes.
6. Vers une codification des mécanismes de complexification et de fonctionnement en tant que lois naturelles :
La tendance à l’augmentation de la diversité et de la complexité dans les systèmes physiques a été examinée en détail dans des travaux antérieurs, tels que la proposition de la première loi de la biologie par McShea et Brandon, dans laquelle ils postulent une loi évolutive de force zéro qui stipule que :
Dans tout système évolutif dans lequel il y a de la variation et de l’hérédité, il y a de la variation et de l’hérédité, il y a une tendance à l’augmentation de la diversité et de la complexité, qui est toujours présente mais qui peut être contrariée ou augmentée par la sélection naturelle, d’autres forces ou des contraintes agissant sur la diversité ou la complexité [18].
Alors que la proposition de McShea et Brandon pour une loi évolutive de force zéro s’applique exclusivement aux systèmes évolutifs dans lesquels il y a variation et hérédité, et est donc étroitement spécifiée aux organismes vivants (qui ont la capacité héréditaire conférée par la mémoire chimique du système ADN-ARN-protéine), les travaux de Wong et al l’étendent aux systèmes physiques génériques, et dans notre postulat sur le réseau unifié de mémoire spatiale, nous décrivons le mécanisme par lequel les systèmes physiques génériques, ou la matière organisée dans l’univers, obéissent à une force d’évolution universelle – y compris l’augmentation constante de l’information fonctionnelle, de l’organisation synergique, de la complexité et de la diversité – par le biais des propriétés de mémoire de l’espace.
Même dans le domaine de la physique purement théorique, dans l’analyse de la théorie de la complexité, il y a eu des propositions de concepts tels que la deuxième loi de la complexité quantique, par Susskind et Brown [19], où il est démontré que longtemps après qu’un système a atteint l’entropie maximale, son évolution n’est pas terminée car au niveau quantique, il continue à explorer l’espace de phase combinatoire et le réseau d’enchevêtrement d’un tel système continuera à se complexifier. Ainsi, la complexité quantique du système augmente avec le temps et ce processus dépasse de loin le temps nécessaire à un système fermé pour atteindre l’équilibre (état d’entropie maximale). Cela a des implications importantes pour la physique des trous noirs, et donc pour la physique holographique et unifiée.
7. La fausseté du progrès :
La théorie évolutionniste conventionnelle en biologie est très défavorable à toute proposition de tendance “intrinsèque” à l’augmentation de la complexité. Il existe une multitude d’exemples de systèmes dynamiques complexes, mais la théorie conventionnelle soutient que l’augmentation de la complexité n’est ni universelle ni inévitable. Smith et Szathmary ont donné l’exemple des bactéries pour illustrer cette conclusion, car de nombreux procaryotes ne sont probablement pas plus complexes aujourd’hui que leurs ancêtres il y a 2000 millions d’années [20]. Ils soutiennent que le maximum que nous puissions dire, en termes d’organisme vivant, est que certaines lignées sont devenues plus complexes au cours du temps. En outre, il existe probablement des exemples, en dehors de la biologie, de systèmes dynamiques complexes qui n’ont pas connu d’augmentation quantitative de leur niveau respectif de complexité, ou de leur contenu en information, après avoir atteint un maximum d’équilibre dynamique. Smith et Szathmary ont ensuite exposé les principales raisons pour lesquelles les biologistes ont tendance à considérer toute théorie d’une augmentation inévitable de la complexité – équivalant à une loi de la nature – comme une déduction erronée et un sophisme, le sophisme du progrès.
La notion de progrès a mauvaise presse chez les biologistes évolutionnistes. Lamarck a accepté l’idée antérieure d’une échelle de la nature et a soutenu que les organismes ont une tendance inhérente à gravir l’échelle. C’est la notion de tendance inhérente à Lamarck, plutôt que sa croyance en l’hérédité des caractères acquis, que Darwin rejetait lorsqu’il déclarait que sa théorie n’avait rien en commun avec celle de Lamarck : il voyait à juste titre qu’expliquer l’évolution par une tendance inhérente est aussi vide que de dire qu’un homme est gros parce qu’il a une tendance inhérente à l’obésité. Aujourd’hui, nous sommes mécontents d’une image de l’évolution qui nous place au sommet et place tous les autres organismes en ligne derrière nous : de quoi pouvons-nous être si fiers ? Pour être juste, l’homme n’était pas du tout au sommet de la scala naturae médiévale ; il y avait des anges et des archanges au-dessus de nous, ainsi que des vers en dessous.
Il existe bien sûr des raisons plus solides, à la fois empiriques et théoriques, de rejeter une image simple du progrès sur une échelle linéaire. D’un point de vue empirique, l’histoire de la vie est mieux représentée sous la forme d’un arbre ramifié que sous celle d’une simple ligne ascendante. Les archives fossiles montrent que de nombreux organismes – les crabes en fer à cheval, le cœlacanthe, les crocodiles, par exemple – ont subi peu de changements, progressifs ou non, pendant des centaines de millions d’années. Sur une échelle de temps plus courte, les espèces apparentées racontent la même histoire. Les drosophiles Drosophila melanogaster et D. simulans sont difficiles à distinguer morphologiquement, mais les données moléculaires indiquent qu’elles sont séparées par plusieurs millions d’années d’évolution. Par conséquent, soit l’évolution morphologique des deux espèces a été presque exactement parallèle, ce qui n’est pas plausible, soit aucune des deux espèces n’a changé.
D’un point de vue théorique, il n’y a aucune raison pour que l’évolution par sélection naturelle conduise à une augmentation de la complexité, si c’est ce que nous entendons par progrès. Tout au plus, la théorie suggère que les organismes devraient s’améliorer, ou du moins ne pas se détériorer, pour faire ce qu’ils font actuellement. Mais une augmentation de la “forme physique” immédiate – c’est-à-dire le nombre attendu de descendants – peut être obtenue en perdant des yeux ou des jambes aussi bien qu’en les gagnant. Même si une augmentation de l’aptitude ne peut être assimilée à une augmentation de la complexité ou à un progrès, il peut sembler à première vue que le “théorème fondamental de la sélection naturelle” de R.A. Fisher (1930) garantisse au moins une augmentation de l’aptitude. Ce théorème stipule que le taux d’augmentation de l’aptitude moyenne d’une population est égal à la variance génétique de l’aptitude : comme les variances ne peuvent pas être négatives, le théorème stipule que l’aptitude ne peut qu’augmenter. Si tel est le cas, la “fitness moyenne” en biologie est un analogue de l’entropie en physique : elle donne une flèche au temps. Ainsi, en physique, l’augmentation inévitable de l’entropie distingue le passé du futur : si l’aptitude moyenne ne peut qu’augmenter, cela définit une direction pour l’évolution. Il semble que Fisher ait effectivement pensé que son théorème pouvait jouer un tel rôle : sinon, pourquoi “fondamental” ? Malheureusement, le théorème n’est valable que si les aptitudes relatives des génotypes sont constantes et indépendantes de leur fréquence dans la population : pour de nombreux caractères, cette constance n’existe pas [ibid, 20].
Ainsi, même s’il existe une tendance – une véritable loi physique – à l’augmentation de la complexité des systèmes dynamiques multi-constituants interagissant intégralement, cela ne signifie pas que chaque instance d’un tel système dynamique augmentera nécessairement en complexité, ce qui n’est donc pas absolument nécessaire ou universel. Certains systèmes dynamiques complexes peuvent atteindre un contenu d’information optimal dès le début de leur constitution et resteront donc relativement immuables dans un optimum d’information.
Conclusion :
La Perspective de la Science Unifiée :
Dans l’étude The Autodidactic Universe [21], on cherche à savoir s’il est possible que les lois physiques elles-mêmes évoluent et changent. Cette question est intéressante car elle permet d’évaluer la raison pour laquelle les lois et les constantes actuelles de l’univers sont plus probables qu’un autre ensemble (connu sous le nom de problème du réglage fin, que nous examinons et clarifions également dans notre étude The Unified Spacememory Network). Ainsi, par exemple, les constantes de couplage de la nature (par ex, la constante gravitationnelle G, ou la constante de structure fine alpha) pourraient s’avérer être des variables dynamiques, et en effet dans l’Origine de la masse et la nature de la gravité [22] il est montré que les propriétés fondamentales telles que la masse, les forces de confinement ou de liaison nucléaires, et la gravité sont basées sur des variables dynamiques qui sont fixées par les conditions de décohérence des fluctuations quantiques du vide couplées à la densité d’énergie du point zéro et à une force de pression de Planck résultante qui découle de l’écoulement du plasma de Planck dans les particules des trous noirs. La dynamique de rétroaction opérant dans ces états fondamentaux est la quintessence des flux d’information qui caractérisent le changement fonctionnel organisé des systèmes en évolution dans l’univers..
Il y a donc certainement des mécanismes qui sous-tendent la complexification de notre univers, et même les forces, les constantes et les lois elles-mêmes, ce qui est une excellente chose car cela signifie que nous pouvons comprendre ces mécanismes fondamentaux et donc comprendre la nature de l’univers à un niveau plus profond. Du point de vue du réseau unifié d’espace-mémoire, dans lequel le temps (la 4e dimension) émerge holographiquement de la propriété de mémoire de l’espace voxélisé en 3D – c’est-à-dire que le temps n’est pas fondamental -, cela ouvre une réflexion intéressante sur ce que l’on entend par “système en évolution” si toutes les coordonnées spatio-temporelles coexistent en même temps. Ce que nous soulignons dans l’étude Spacememory Network, c’est que la nature intrinsèquement atemporelle de l’univers et sa nature intrinsèquement non locale (comme l’illustre facilement la théorie quantique) signifient qu’il y a une diaphonie continue dans les systèmes “évolutifs” entre leur état initial et des états beaucoup plus avancés de grande complexité fonctionnelle, et qu’il y a donc un échange d’informations transtemporel qui est la force d’ordre néguentropique dans l’évolution et le développement des systèmes physiques. La trajectoire évolutive d’un système donné n’est que la projection holographique de son réseau neuromorphique sous-jacent de connectivité de l’information, c’est-à-dire le champ morphogénique et, en fin de compte, le changement, comme le temps, est illusoire.
Références :
[1] E. J. Chaisson, “A unifying concept for astrobiology,” International Journal of Astrobiology, vol. 2, no. 2, pp. 91–101, Apr. 2003, doi: 10.1017/S1473550403001484.
[2] A. Mistriotis, “A universal model describing the structure and functions of living systems,” Communicative & Integrative Biology, vol. 14, no. 1, pp. 27–36, Jan. 2021, doi: 10.1080/19420889.2021.1887549
[3] M. L. Wong et al., “On the roles of function and selection in evolving systems,” Proc. Natl. Acad. Sci. U.S.A., vol. 120, no. 43, p. e2310223120, Oct. 2023, doi: 10.1073/pnas.2310223120.
[4] T. Westby and C. J. Conselice, “The Astrobiological Copernican Weak and Strong Limits for Intelligent Life,” ApJ, vol. 896, no. 1, p. 58, Jun. 2020, doi: 10.3847/1538-4357/ab8225.
[5] S. A. Kauffman, The Origins of Order: Self-organization and Selection in Evolution. in The Origins of Order: Self-organization and Selection in Evolution. Oxford University Press, 1993. [Online]. Available: https://books.google.com/books?id=lZcSpRJz0dgC
[6] A. J. Watson, “Implications of an Anthropic Model of Evolution for Emergence of Complex Life and Intelligence,” Astrobiology, vol. 8, no. 1, pp. 175–185, Feb. 2008, doi: 10.1089/ast.2006.0115.
[7] Meijer D K F, Wong KW, 2022. How the Universe Orchestrated the Conditions for First Life, using an Informational Quantum Code. The Concerted Action of Magnetic Monopole and Photon/Phonon Fields through a 5D Symmetry Breaking. https://www.researchgate.net/publication/357312383_How_the_Universe_Orchestrated_the_Conditions_for_First_Life_using_an_Informational_Quantum_Code_The_Concerted_Action_of_Magnetic_Monopole_and_PhotonPhonon_Fields_through_a_5D_Symmetry_Breaking
[8] Sheldrake, R. (2009). Morphic Resonance: The Nature of Formative Causation. Ukraine: Inner Traditions/Bear.
[9] M. C. Parker and C. Jeynes, “Maximum Entropy (Most Likely) Double Helical and Double Logarithmic Spiral Trajectories in Space-Time,” Sci Rep, vol. 9, no. 1, p. 10779, Dec. 2019, doi: 10.1038/s41598-019-46765-w.
[10] N. Haramein, W. D. Brown, and A. Val Baker, “The Unified Spacememory Network: from Cosmogenesis to Consciousness,” Neuroquantology, vol. 14, no. 4, Jun. 2016, doi: 10.14704/nq.2016.14.4.961.
[11] W. Brown, “Provisional Definition of the Living State: Delineation of an Empirical Criterion that Defines a System as Alive,” Qeios online journal, preprint, Jul. 2023. doi: 10.32388/V5EDGF.
[12] A. Mistriotis, “Mathematical and physical considerations indicating that the cell genome is a read-write memory,” Progress in Biophysics and Molecular Biology, vol. 178, pp. 50–56, Mar. 2023, doi: 10.1016/j.pbiomolbio.2023.01.006.
[13] A. Wagner, Arrival of the Fittest, New York City: Penguin Group, 2014.
[14] M. Levin, “The Computational Boundary of a ‘Self’: Developmental Bioelectricity Drives Multicellularity and Scale-Free Cognition,” Front. Psychol., vol. 10, p. 2688, Dec. 2019, doi: 10.3389/fpsyg.2019.02688.
[15] R. M. Hazen, P. L. Griffin, J. M. Carothers, and J. W. Szostak, “Functional information and the emergence of biocomplexity,” Proc. Natl. Acad. Sci. U.S.A., vol. 104, no. suppl_1, pp. 8574–8581, May 2007, doi: 10.1073/pnas.0701744104.
[16] Mistriotis A. Self-similarity in living systems. Amazon. com Inc.; 2018 [accessed on November 11, 2023]. Kindle e-book: https://www.amazon.com/Self- similarity-Living-Systems-Antonis-Mistriotis-ebook /dp/B07G2DVMDL
[17] D. W. McShea, Functional complexity in organisms: Parts as proxies. Biol. Philos. 15, 641–668 (2000).
[18] Daniel W. McShea and Robert N. Brandon, Biology’s First Law: The Tendency for Diversity and Complexity to Increase in Evolutionary Systems. Chicago and London: The University of Chicago Press, 2010.
[19] A. R. Brown and L. Susskind, “The Second Law of Quantum Complexity,” Phys. Rev. D, vol. 97, no. 8, p. 086015, Apr. 2018, doi: 10.1103/PhysRevD.97.086015.
[20] J. M. Smith and E. Szathmary, The Major Transitions in Evolution. OUP Oxford, 1997
[21] S. Alexander et al., “The Autodidactic Universe,” arXiv:2104.03902 [gr-qc, physics:hep-th, physics:physics, physics:quant-ph], Mar. 2021, Accessed: Apr. 16, 2021. [Online]. Available: http://arxiv.org/abs/2104.03902
[22] Nassim Haramein, Cyprien Guermonprez, & Olivier Alirol. (2023). The Origin of Mass and the Nature of Gravity. https://doi.org/10.5281/zenodo.8381115









